S A C R E D G E O M E T R Y I N A C C O U ST I C S
S O U N D M A D E V I S I B L E
By Sacred Geometry Fibonacci Sequence Explains Secret To Life Documentary
Before coming in to the subject of accoustics and music I would like to deliver a short introduction to some of the main objectives around the patterning of the energy fields in nature and cosmos, presented in this pedogically instructive video:
Quoting its speaker:
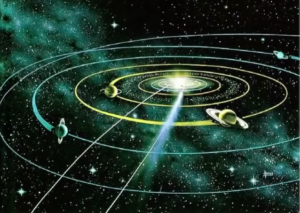
From observing the movements and positions of the stars and the planets; the sun and the moon, people have since long noticed that the stars are making up certain specific constellations. And also by watching the days turn into nights, and the nights turn to days and the seasons as coming and going, we do become aware of that rythmical pattern that we call time. Thats the slower rythms in our human lives. Other, but much faster are the heartbeats and the two-beats of walking (ONE two, ONE two, ONE two)

In human bodies as well as in the tigers stripes you may see some symetrical patterns, and the same patterns are also used when wee create art or buildings.

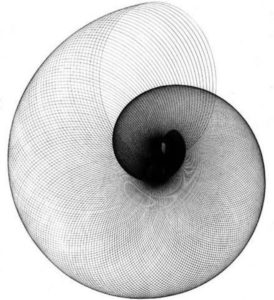
These patterns show a remarkable simularity.Why should a spiral of a shell be so similar to a sprial of a galaxy?

Mathematics is a powerful tool when scientists seek to understand the patterns of our world. By quantifying their observations and using mathematical techniques to examine them, they might discover the underlying causes to nature´s rytms and regularities.
And so far it has worked to reveal the secrets behind the eliptical orbits of the planets, as well as for example the electromagnetic waves that connect our cellphones. Mathematics has guided the way - leading us even right down to subatomic the building blocks of matter; which rises the question; Why does it work at all? Is there an inherit mathematic nature to reality or is the mathematics just in our heads? (Bateson)
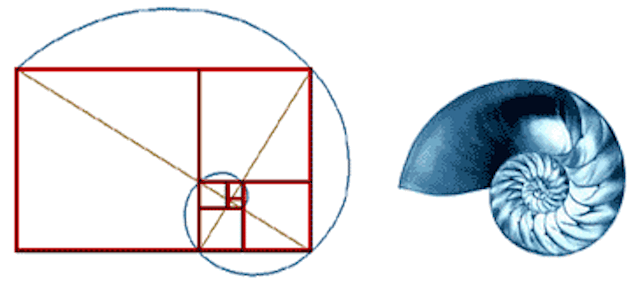
Although nobody so far has been able to substantiate the findings with complete scientifical explanation, (commented by the Swedish mathematician and physisist Helena Granström) the ratio called φ and the sequenses of numbers called the fibonacci-serie have been of great help to reveal the underlining patterns that connect, to talk with Batesons words. Its quite an enigma why and how, but the seemingly random series of numbers, known as the "fibonacci sequence"; discovered and worked out by the Leonardo Fibonacci in the 13th century (who was considered to be the most talented Western mathematician during the Middler ages) has turned out to be able to facilitate a lot of understanding of how things work in nature and the universe; on macro- as well as micro level.
These are questions that the mathematician and astrophysist Mario Livio, who is the author of the book; Is God a mathematician, has been wrestling with. Fascinated by the often deep and mysterious connection between mathematics and the world, he is demonstrating how there are numbers all around us in nature, not at least in the numbers of the petals of the flowers, which often are the same as in the fibbonacci-sequence. This seemingly arbitrary set of fibonacci numbers gives us clues to how things work in nature. While most of these relationships remain unproven, there is no doubt that evolution seems to favour these numbers, as it appears so frequently everywhere in nature. And Mario Livio demonstrates here how φ even play a role in

Statistically the fibonacci-numbers do appear a lot. Christoffer Golé Smith at College, says. If you look at the bottom of a pine cone you will see spirals making up fibonacci-numbers in both directions. The same is true of the seed in the sunflower head. It has two sets of spirals, and if you count the spirals in each directions you will find that both count fibonacci-numbers.


Anything that involves waves will have φ in them, as for example here, light- and soundwaves.
 φ tells us what color will appear in the rainbow, and how middle "c" on the piano should sound.
φ tells us what color will appear in the rainbow, and how middle "c" on the piano should sound.

Or in the light of a supernova

We know that these phenomena are mathematically related to one another, but it is not always obvious how or why.
φ just seems to reveal a hidden but deep order to our world. And this raises some intriguing questions:
While there are some theories explaining the fibonacci patterning connections, it still rises some intriguing questions, as for example if plants do know mathematics, to wich the physisist Christoffer Golé Smith has the short answer: -No, they don´t need to know math. In a very simple geometric way they set up a little mashine that creates the fiboncci-sequences, in many cases. (I think this question id a bit odd though as would also Bateson had done)
there an inherit mathematic nature to reality, or is mathematics all in our heads, is the somewhat remarkable question thats asked by the scientists in this video. And to that I at least know what Gregory Bateson would ´have answered.
Hoping to find the underlying causes to the rytm and regularities of nature, the scientists of today continue to ask questions like this.The seemingly arbitrary progression of the fibonacci series of numbers fascinates many, and although its representation of fundamental processes in nature and cosmos remains unproven, its curiois to see how surprisingly often it appears as the basic formula of patterning the processes in nature and cosmos.
The mysterious connection between the physical word and mathematics run deep. We all know the world Pi from geometry;
φ = the ratio between the circumference of the cirkel and its diameter.

And that its decimals digits continue for ever without repeating a pattern, as about 2013 it has been calculated to 12,1x 10 trillion digits
Somehow φ is a whole lot more. -It appears in a whole host of other phenomena to says Mario Silvio, who at least of the face of it has got nothing to do with circels or anything. For example it appears also in probability-theory quite a bit, which he the demonstrates with a little experiment. Even though there are no circles here, no diameter or something, its really amazing how φ although seem to play a part in it. Since φ applies to round objects like cirkels, it can show up at the strangesat places. Some see it in the meandering patos of rivers.
φ appears everywhere in nature and cosmos even in the relational patterning in a series of mountaintops. We know that there is aconnection between shapes of this kind, but it is not always obvious how.

IN THE REALM OF ACCOUSTICS OR MUSIC THE PATTERNING OF
SACRED GEOMETRY BECOMES YET MORE EVIDENT
For those of who want to learn more about how the infinite numbers of φ represents an infinite series of fibonacci-related spiraling waves getting increasingly nearer infinity itself, without loosing its deviation from it totally; but causing the waving movements to become infinitely increasingly smaller and smaller, I recommend the more advanced course on the subject held by Stephen Skinner on Youtube and introduced on my Website here »
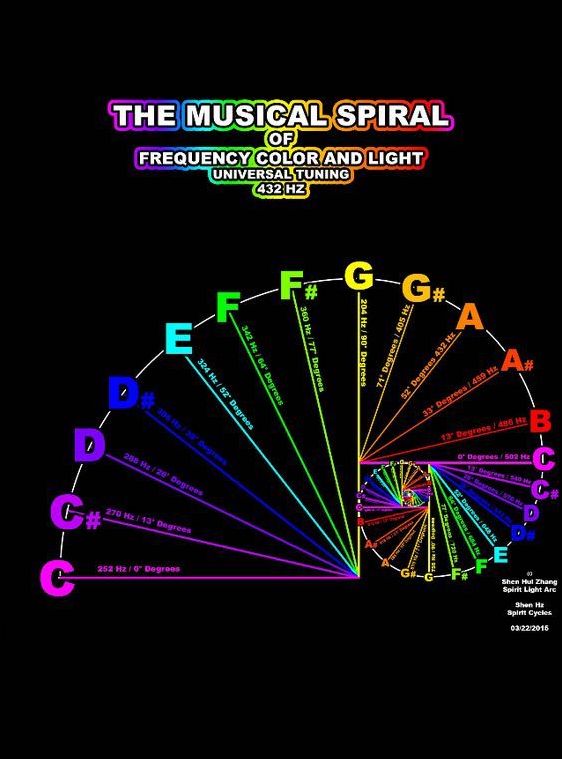
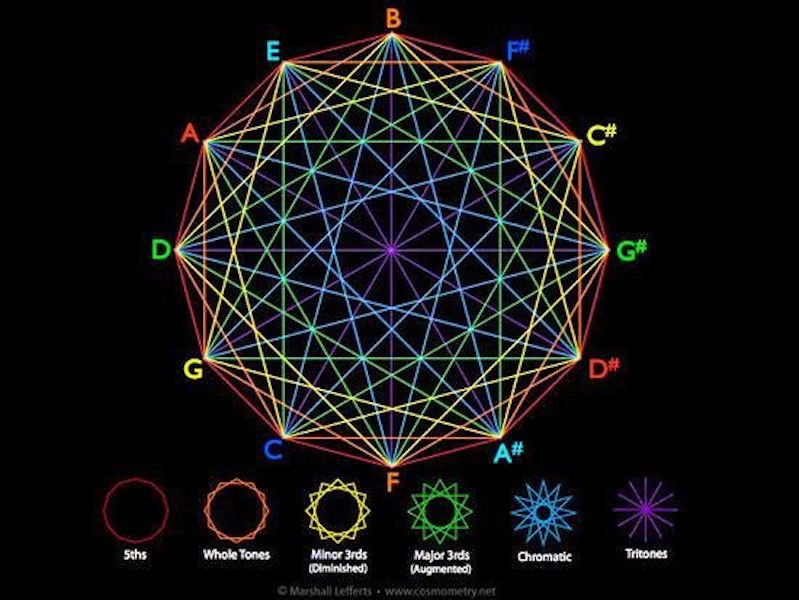
That is namely crucial for to be able to understand how the cromatical scalesystem, pictured her beneath as a spiral, functions and why for exampel a fifth in the first octave doesn´t represent exactly the same ratio as in higher or lower octaves. These small deviations which alterate over the octaves give rise to the spiral shape that´s representative for the overall patterning of the energy fields in nature and cosmos called a vortex:

In this video Adam Neeley tells us the fact that mass and energy are the same thing, but only att massively different scales. Related to the music theory of relativity this tells us that rythm, melody and harmony are the same thing, just on similarily massively different scales.
If a wave-form repeat regurlarily over a period of time, we will perceive that waveform as having pitch; periodicity. If one speeds up a regular pattern of a pulse beat enough many times, you will get a pitch. This is a pretty normal phenomenon we all know intutively about; when a motor of some kind start to speed up you will perceive a tone; or a pitch.
The mindblowing thing is when we start to apply this on harmony. - What if I told you, that harmony is nothing else than highly complex interlocked polyrythmics, i.e. harmony literally is rythm? Adam says
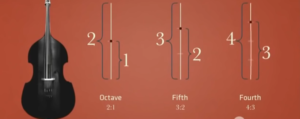
Interval is the difference between two pitches, and can be described as simple ratios. In between these to notes you have a so called perfect fifth whose ratio is 3/2
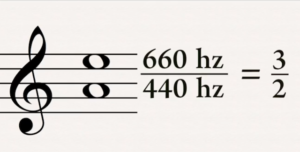
So if you for example play the tone "c" and compare it with the tone "g" which is situated five intervals higher up on the scale from "c" on a guitarstring you will meassure the difference in the length opf the string is shown on this picture.
What Adam thereafter shows is quite amazing, for me, as I have been out on the hunt of knowing more about the phenomemenon two against three since quite long now. I have always had a feeling of that it is something almost mysterious and / or very special with the two against thre ratio in polyrythmics.
If you take the polyrythm two against three and speed it up enough much you will simply achieve the harmony of a fifth.

Here on this video you can easily get a grasp of what kind of polyrythm two agains three makes up. You beat two beats the left hand and three in the right hand »




Here in the beginning of this video you can listen to a typical two against three-beat, which mostly, together with yet more complex poly-rythmics as for excample three against four-beat, makes up the fundamental pattern in most African Music.
SAMARBETE MED NATUREN KONTRA MOTSATSEN
Man kan undra mycket över meningen med musik och dess funktion i naturen / kulturen och kosmos/ skapelsens tillkomst och det är det många som har gjort, inte minst de antika greker som tillsammans med pythagoras upptäckte hur vissa bestämda talförhållanden låg till grund för harmoniska intervall och dess motsats, dessa upptäckter som då också antogs gälla som någon slags lagbunden urkraft i kosmos och kallades för “Sfärernas musik”
Akustiska svängningar dvs de fysiska fenomen som ger upphov till att vi uppfattar ljud med vår mänskliga perception är helt och hållet fysiskt påtagliga fenomen som vid kontakt med magnetfält skapar bestämda specifika mönster beroende på dess svängningstal, och det har också bedrivits experiment för att undersöka möjligheten att få föremål att levitera med hjälp av akustiska vibrationer.
Det finns nämligen också de som Michael Tellinger menar att vissa kulturer i Sydafrika under tidigare högtstående kulturer har haft kunskap om hur man får stora stenblock att levitera med hjälp av konformade föremål som antas ha varit utformade så att de innehar en sådan levrande potential.
Olik matematiskt ocfysikaliskt sinnade musiker och ingenjörer ägnar sig åt att skapa musik ur fibonaci talserien och får på så sätt fram fantastiska fractalmönster och eller häftiga kompositioner som denna; ngt av det vackraste jag hört på länge:
Inom musikpsykologin har det bedrivits mycket intressant neuropsykologisk forskning varvid inte minst samspelet barn / mor / musik undersökts varvid det kunnat visas att foster redan vid ålder förmår uppfatta ljud och reagerar starkt på akustiska stimulin.
Och ju mer man tränger in i musikens mysterier ju mer framgår det hur basal dess funktion måste antas vara i naturen såväl som i den mänskliga kulturen inte minst i form av att utgöra ett slag akustiska kupoler som innesluter individerna i ett rum av en gemensamt åstadkommen “ljudorgel” och / eller som en akustisk förlängning av navelsträngen mellan mor och barn.
När jag sökt efter information om dessa ting online har jah kommit över så mycket spännande info om nya samband kors och tvärs att det skulle ta en livstid att utforska även det. så det får jag lägga på hyllan till nästa liv. Men efter att jag blivit undervisad om hur mycket en dodekadron kan inrymma av andra geometriska former - dvs i stort sett alla efter vad jag kan förstå
Jag börjar med detta i min redogörelse av “de sk “Pygmy”-folkens, bosatta i Central- Afrika´s regnskogar, kultur eftersom den till så stor del handlar just om musik och en mycket komplexe utarbetad sådan
“The Pyramid is a puré christall”
If you multipla the frequenxe the struktur of the matter will change
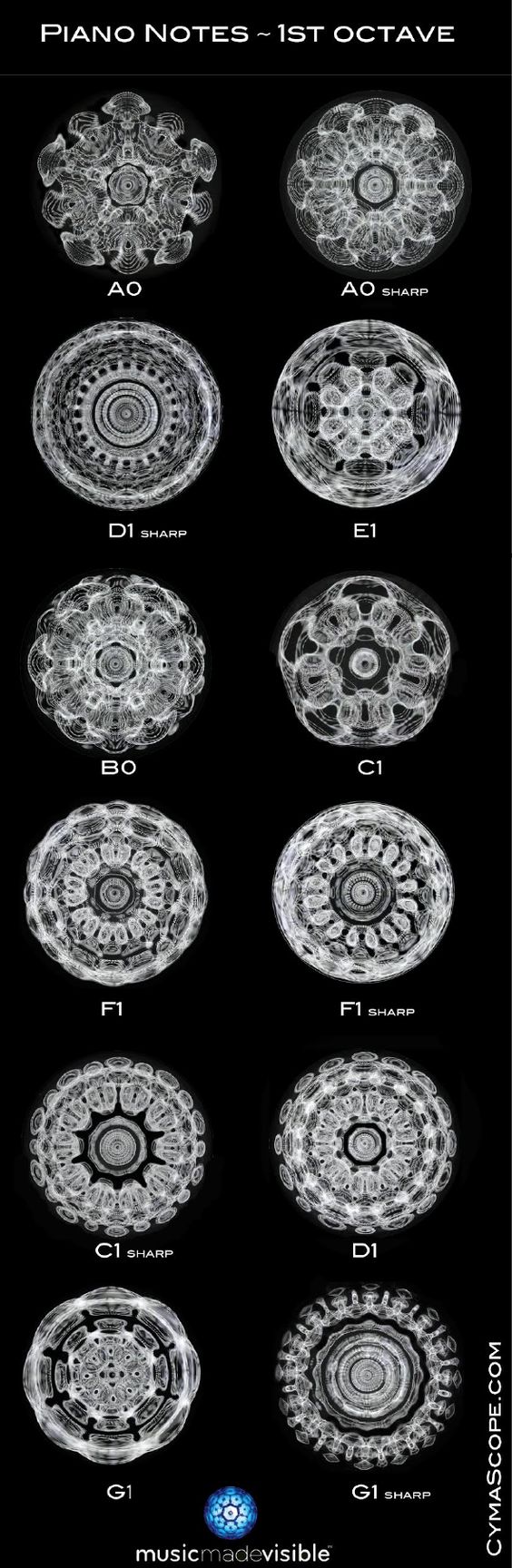
Ancient Knowledge Pt 1 Consciousness, Sacred Geometry, Cymatics, Illusion of Reality Rare Footage
Oscillating a wine-glass by playing sound at its resonans frewuency will cause itt to move. Change and liquify its structure and evbentually even break it.
This is what primitive people would call “magic”. I´m not talong about magic tricks, but rather unseen forceds at work.
SOUND IS THE BASUS OF FORM AND SHAPE
In the besinning was word and the word was god
Into the void of space came sound and matter took shape.
Everything in existence is the result of a frewuency the Bible tells us that the beginning was the word and the word was god.
word=symboloic
Are you beginning to see tyst there is much more to life than you can perceive with your 5 senses
Each material has its own special way of behaving
Claude Lévi Strauss neclear vision 1 - 0
Fact in Nature; 2 against three
SOUND MADE VISSIBLE
Singing in a tonoscope
Ancien sacred geometri
MATTER DOES NOT EXIST
THE CONCET OF SUBSTANCE
ARE THE PHILOSOPHIE OF ARISTOTLE
The fact that the is matter is
The Substance of univers is consciousness
Beleive that the substans of the universe is matter leads to
feer greed economy, as peopl of desperation accumulate
therefore its behavoiur that´s important
Quantum physics has shown that timme and space are illusions of our perceptions
The atom is almost entirely empty space
The twelve surroiunding the thirteenth
kubeoctahedron 2:22:31 compoised by Square and triangulär faces
Plus och minus manligt och kvinnligt
Dela blir mer och mer abundnce of the goddess
TVÅ mot Tre i början av videon
Whats so remarkable with the Mandelbroth set is that although it infentely complex its bases on incredible simple principles abnyone who can add and multipla can unsderstand the principle on which its based the problem oss only that you have carry out this operation of adding and multiplicationsto multipla milioons and miljons of times to garn a complerte set
He couldnbt measure its lenght and not its volymer but something in bretween 2 and the yes Mandelbroth said frsctals have.
He cuuldnp messauee its length but its rouhness. 06 - 07 iteration computer . Veta big long effort
Gaston Julia a simplöe equation iteration
The srious of numera you get is called a sett. By hand you could really not know what a set look like
The ighe
Thee dimensions is a cube
Gyllne snittet
Matematik är ett språk.
Pytagoras, och kanske framför allt Euklides, beskrev hur olika proportioner förhöll sig. Bokstavligt handlar det om hur man delar en linje av en viss längd på det mest harmoniska vis som går... Frågan är om det gyllene snittet är verklighet eller inte... men de lyckades skapa en matematisk dikt som har fascinerat eftervärlden. Så enkel, så exakt, så expanderbar. Dikten beskriver vår omvärld med precis den exakthet, eller brist där av, som gör att man undrar om det är sant eller inte... Förnära för att vara lögn. Lite för avvikande för att vara absolut sanning. Tveklöst matematisk vacker prosa.
Pytagoras och Euklides efterföljare har utvecklat teorin in absurdum... Det har tidvis till och med varit ett gudomligt teorem! (För att kontra Skenbild:s lallande om ”ramverk”. Skenbild hade bränts på bål under medeltiden... ;0))!
Även om gyllene snittet kan tillämpas på oändligt olika sätt, så har man som fotograf lättast att tillämpa Fibonaccis teorier. 3:je dels regeln kommer från Fibonaccis.
2/1=2
3/2=1,5 Tredjedelsregeln
5/3=1,6667
8/5=1,60
13/8=1,625
(13+8)/13=21/13=1,615
Every one who is familiar with art knows about the phenomenon called "Golden ratio" and the fibonacci-serie, as it makes up the kind of meassurement that you use in order to accomplish a wellbalancred composition, with the centre stage not in thre middle of the image but at the place where the Golden ratio is situated. This meassurement you might calculate with the help of the fibonacciserie, and thereby achieve the ratio thats called PI . And the funny thing with PI is, according to the astrophysisist and in this video is that you miight fins this kind of relationship in every kind of formation in nature as well as in slump
Sacred Geometry Fibonacci Sequence Explains Secret To Life Documentary
http://hum.gu.se/aktuellt/Nyheter/fulltext//genusperspektiv-pa-vikingatiden-intresserar-ny-professor.cid1208375
_________________________________________________
Scientists Find ‘Evidence’ of a Multidimensional Universe Inside Our Brain
http://upliftconnect.com/multidimensional-universe-inside-our-brains/
Scientists Discover Biophotons In The Brain That Could Hint Our Consciousness is Directly Linked to Light!
http://www.liberospirito.org/Testi/M.Gimbutas/Charlene%20Spretnak%20-%20Anatomy%20of%20a%20Backlash.pdf
För att det ska kunna åstadkommas en spin-rörelse som spiraliserar med eller motsols måste det till någon slags dragning åt ena eller andra hållet i rörelsen, dvs
Huge vänster
dear syncope förenklad
THERE IS NO PARITY: CHIEN-SHIUNG WU
There Is No Parity: Chien-Shiung Wu
Overwigh of right or left hand inducing a slight tension in order to initiate the spin
How Hunter-Gatherers Maintained Their Egalitarian Ways
The important lessons from hunter-gatherers are about culture, not genes.
Today it seems to be quite a few anthropologists as well as evolutionary psychologist, paleolingvists, musicethnologists and others who are carrying out research about the forest-living Pygmy-peoples in Central Africa and Southeast Asia, producing a body of findings that all of it seem to underpin the theories of Maria Gimbutas about the peaceful egalitarian female / mother-centered culture that characterised Old Europe very well and thus at last would have the potential to take the sting out of the attacks against it once for all.
The research that I will refer to in my report of this forest living peoples are made by Phil Dr Jerome Lewis as well as the evolutionary psychologist Peter Gary, the former having written the dissertation
http://discovery.ucl.ac.uk/18991/
http://online.liverpooluniversitypress.co.uk/doi/abs/10.3828/hgr.2015.2
Jerome Lewis: Woman’s Biggest Husband is the Moon: How Hunter-gatherers Maintain Social Equality 25 November 2014
__________________________________
Gyllenesnittet är: den mindre delen är som den större delen i förhållande till det hela. A4 t ex den nedre kanten är gyllene snittet i för hållande till sidan/ höjd till bredd. Din navel ( allas) sitter på gyllene snittet i förhållande till din längd 🙂
Alla plåtslagare kan detta mått utan att veta det- annars kan de inte vika kanter. Alla konstnärer och de som jobbar med harmoni- naturen osv- använder det. Det är en känsla man har i sig när man jobbar - men det går att ta upp till ytan rent praktiskt.
Talserier finns också altifrån Pytagoras som tyckte allt var siffror och så Fibunachi 1+1är2 1+2 är 3, 2+3är 5, 3+5=8 , 5+8 =13, 8+13=21 osv det går rätt fort sen med större tal. Corbusier gjorde ett eget måttband baserat på människans grundmått.
Gyllene snittet kan du googla på för mer historiska kunskaper i musik, /strängar rytmer osv.
Jag undervisar efter olika system om hur man hittar förhållanden till varandra i modell o porträttmåleri- alla elever lär sig "syfta" mellan förhållanden- benet till stolen , stolen till rummet, rummet till kroppens placering. Hoppas du inte blir helt uttröttad av detta basutbud från en målare som själv målar direkt på duken utan både skisser o förstudier det kallas för "a la prima" måleri 🙂
Händer efter timmars sittning att folk frågar : nu kanske det är klart snart? och jag just innan strukit ut det hela och börjat om från början- fast inte jämt. Detta förhållningssätt tror jag har med min frihet att göra.
Kerstin
There Is No Parity: Chien-Shiung Wu
Hold out your hands in front of you, palms forward. They look quite similar, but I’m sure you’re all too aware that they’re actually mirror images of each other. Your hands are chiral objects, which means they’re asymmetric but not superimposable. This property is quite interesting when studying the physical properties of matter. A chiral molecule can have completely different properties from its mirrored counterpart. In physics, producing the mirror image of something is known as parity. And in 1927, a hypothetical law known as the conservation of parity was formulated. It stated that no matter the experiment or physical interaction between objects – parity must be conserved. In other words, the results of an experiment would remain the same if you tired it again with the experiment arranged in its mirror image. There can be no distinction between left/right or clockwise/counter-clockwise in terms of any physical interaction.
Dr. Wu working with a particle accelerator via Biography.
The nuclear physicist, Chien-Shiung Wu, who would eventually prove that quantum mechanics discriminates between left- and right-handedness, was a woman, and the two men who worked out the theory behind the “Wu Experiment” received a Nobel prize for their joint work. If we think it’s strange that quantum mechanics works differently for mirror-image particles, how strange is it that a physicist wouldn’t get recognized just because of (her) gender? We’re mostly here to talk about the physics, but we’ll get back to Chien-Shiung Wu soon.
THE END OF PARITY
Conservation of parity was the product of a physicist by the name of Eugene P. Wigner, and it would play an important role in the growing maturity of quantum mechanics. It was common knowledge that macro-world objects like planets and baseballs followed Wigner’s conservation of parity. To suggest that this law extended into the quantum world was intuitive, but not more than intuition. And at that time, it was already well known that quantum objects did not play by the same rules as classical objects. Would quantum mechanics be so strange as to care about handedness?
By the time the 1950’s rolled around, physicists were smashing subatomic particles into one another in high speed particle accelerators and analyzing the resulting explosion of new, sometimes previously undiscovered particles. One of these previously undiscovered particles was quite puzzling – the K meson. It appeared that there were two different versions – one would decay into 2 pi mesons and the other would decay into 3 pi mesons. Pi mesons are also called pions. All other properties of the K meson were identical, suggesting there was only one type.
Setting up the Cobalt-60 parity test via NIST.
After doing the math, it was determined that the pions in the two and three particle systems must have opposite parity. And according to Wigner’s conservation of parity, there therefor must be two types of K mesons – one that produced two pions and one that produced three pions. Conservation of parity would not allow both systems to come from a single particle.
But what if Wigner’s parity theory were wrong? The K mesons were produced during weak force interactions when protons were smashed into heavier nuclei. In 1956, physicists T.D Lee and C.N. Yang suggested that weak force interactions might not follow the conservation of parity, and that there was indeed a single K meson. That the two systems of pions were the result of a single K meson that had a definable parity, and that parity was not conserved in this particular case. Consider if the K meson had a spin, and that a clockwise spin produced the 2 pion system and a counterclockwise spin produced the 3 pion system. This would be an example of a violation of the conversation of parity. A violation that physicist were suggesting was occurring with the K meson.
An experiment was derived to put parity to the ultimate test.
COBALT-60
As you can imagine, these kinds of experiments are a bit complicated. And it’s my mission to break complicated things down to the point that your everyday curious hacker can understand. The goal is to prove that Wigner’s conservation of parity did not hold water with weak force interactions. To do this, we’re going to need three things:
1 Something that emits beta radiation (beta decay is caused by the weak force).
2 Something that has two known physical states.
3 A way to measure the radiation in each of the states.
Cobalt-60 parity test apparatus via NIST.
Conservation of parity would insist that the measured radiation be the same in either state. Because if parity is to be conserved, it should not be possible to get a different experimental outcome between different states, like spin for instance. This can be done by taking Colbalt-60, which is naturally radioactive and cooling it to a smidgen above absolute zero. Cooling it to this temperature takes away most molecular motion, and allows the atoms to arrange themselves in a crystal structure while in the presence of a very strong magnetic field. The magnet field also polarizes the Colbalt-60 nuclei, which means they spin in the same direction parallel to the magnetic field.
Now all we have to do is:
1 Measure the beta radiation intensity.
2 Reverse the magnetic field direction.
3 Measure the beta radiation intensity.
4 Compare the results.
By reversing the magnetic field, we cause the cobalt-60 nuclei to reverse polarization. Conservation of parity says there should be no measurable difference between the two physical states. And I’m sure you can guess by now what they found – the measured beta radiation intensity was greater in one direction. This was the nail in the coffin for Wigner’s parity theory. It allowed physicists to reexamine results of previous experiments involving weak force interactions and helped advance quantum theory and eventuality lead to the Standard Model of particles we have today.
CHIEN-SHIUNG WU
As we mentioned above, Lee and Young received the Nobel Prize for the Wu experiment. Wu, unfortunately, didn’t. Wu was one of a handful of female physicists during that time whose name and research are not as well known as they should be. Gender-based injustice was widespread during her time, but she would receive worldwide recognition for her contributions to nuclear physics from the 70’s onward.
Indeed, she was awarded the inaugural Wolf Prize in Physics in 1978, partly to make amends for the Nobel slight, but also for her further work in experimental nuclear physics. Wu also worked on the Manhattan Project, held a prestigious chair at Columbia University, and was responsible for important experimental results in exploring the weak nuclear force and the first experimental confirmation of quantum photon entanglement.
Chien-Shiung Wu died in 1997 at 84. Let’s close with a fitting quote from Dr. Wu during an address at an MIT symposium in 1964:
“I wonder whether the tiny atoms and nuclei, or the mathematical symbols, or the DNA molecules have any preference for either masculine or feminine treatment.”
Posted in Featured, History, Original Art
Tagged Nobel, parity, particle accelerator, physics, quantum physics
I love the music of these much misunderstood people whose music is so deeply attuned to the music of nature and the forest itself. It resembles a little - just a little - the traditional music of the Papua New Guinea forest dwellers, which has virtually disappeared because of misguided Christian missionary prohibitions. Gathering all this traditional music is a most valuable and worthy task. Thank you very much for it.
When I was dealing with the subject I was planning to manage in my bachelor thesis in musicpsychology; namely the inner imagery being expressed in the paintings of my schoolchildren, as well as unfolding by itself, as a sheer mystery out of my own control; just like in the dreams, when I attended the kind of psycho-therapy that´s called GIM-therapy I was searching for a suitable word for the elevated feelings of sorrow and pain as well as pure joy and solemness and at last made up my mind for to use the word “numinous”. And just the other day I discovered that that is also the word that the religion historian Eliade is using to describe what kind of experience one might conclude is expressed in prehistorical representations as the one Maria Gimbutas deciphered as different kinds of “goddesses” or just sacred “numinous” representations for
That´s interesting aspect to apply to the cultural events described so well by Jerome Lewis in his lecture at RAG to have in mind when visiting theses remote inner worlds in the imageries of the forest living hinterland gatherer.
In his more elaborate scientific writings he come closet the reasonings I pursue in my first kiss of my subject: Complete analogue gestalts.
And when I yesterday discovered the article
And this was the map I then drew to demonstrate how such numinous experiences are thought to be generated in our minds to showw that what might att first look quite simple and selevident, quite the contrary is quite complex
that I had discovered was working all on its own without my own control or will when I was about in the discipline of musicpsaychology, which is a discipline that
Transcending Paradox: The Chinese “Middle Way” Perspective∗
Abstract. Western thought is noted for its strengths in categorization and analysis; Eastern, or Chinese thought, is noted for its integrative and encompassing nature. This article seeks to bridge the two. Specifically, it aims to enrich Western thinking and the existing body of paradox literature by proposing the idea of paradoxical integration, a concept derived from the Chinese middle way philosophy. Paradoxical integration, the notion that two opposites (such as “self” and “other”) may be interdependent in nature and together constitute a totality (“integration”), is introduced as one means of transcending paradox and the conventional Western conceptualization of exclusive opposites. It suggests how we can apply the concept of interdependent opposites in a both/and framework to foster reconciliation of the apparent polarities of such dichotomies as competition and cooperation. The article concludes with a discussion of the broad implications of the concept of paradoxical integration upon both academic research and business practice.
https://faculty.darden.virginia.edu/chenm/2007AOM_Workshop/pdf/session6/Transparadox%20APJM02.pdf